Why do waves always come towards the beach?

Have you ever noticed that the waves always come towards the shore at the beach?

That's quite strange right? A storm out in the ocean will generate waves and they will travel radially outwards from the source, so how come we never get to see the waves coming in at an angle? Should we not occasionally be able to walk beside the waves as they move parallel to the coast?

The answer is refraction:

As a wave moves into a medium where it is slower it will bend towards the slower material. You can think of it like a line of people holding hands walking through a meadow. Part of the line reaches a marsh and is slowed down. The people in the meadow are still moving faster and so the line starts to bend. By the time everyone is in the marsh, the line has changed direction.

One reason you could expect waves in shallow water to be slower is bottom drag. Viscosity (friction, drag) is important, it changes the shape of waves and the motion of the water in them. However, even when we discount it, waves still travel more slowly in shallower water. It is this confusing fact that I am going to explain intuitively.

⚠️This is going to involve some equations but they are not essential for understanding the ideas.⚠️

Let's consider water waves in 2D:

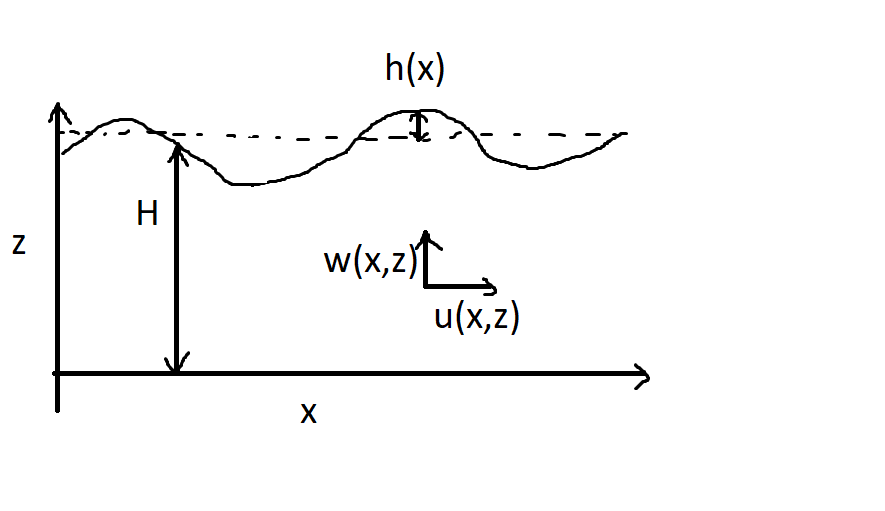
We have H the average water depth, h the deviation from H and u and w the horizontal and vertical velocities of the fluid.

There is no water coming in from the sea floor or from the surface so the total amount of water flowing into any column of water can only be the net flux in horizontally. Mathematically, this is written

$\frac{\partial h}{\partial t} = -\frac{\partial}{\partial x} \int u \, dz .$

Let's assume that vertical accelerations are much smaller than horizontal ones. We can imagine extreme scenarios where this wouldn't be a good assumption but for the average beach waves, it works fine. Newton's second law says that if there is no acceleration in a direction, then the forces in that direction must be in equilibrium. The two forces acting on our shallow waves are gravity and pressure.

Pressure represents how hard molecules are bumping against each other. If we keep a fluid at high pressure this does not imply there will be flow. The fluid is accelerated when there is a gradient in pressure. To again use people as an analogy, pressure might correspond to the density of people in a crowd of introverts. As the introverts enter an area with fewer people they will experience a force pushing them away from the crowd and into the more dispersed people.

These two forces, gravity and the pressure gradient, must be in balance. This is called the hydrostatic assumption and can be written

$p = \rho g (H + h-z)$

where p is pressure, rho is density and g is gravity.

We have established there are only two forces acting on the fluid. Gravity is only in the vertical direction, so pressure gradients drive the horizontal flow. How do we generate a pressure gradient? When the surface height increases there is more water above one point than its neighbours. This means that the pressure below it is higher and so water is pushed out of the region. We can express this mathematically using the material derivative:

$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + w\frac{\partial u}{\partial z} = -\frac{1}{\rho}\frac{\partial p}{\partial x} = - g\frac{\partial h}{\partial x}.$

Notice that the only thing that accelerates the fluid is the change in surface height. We are assuming the bottom boundary is not able to drag the fluid (neglecting viscosity) so it doesn't matter how deep the water is. No matter what depth you are looking at the gradient in pressure caused by the different heights at the surface will be the same. Thus, the horizontal velocity u is independent of z!

Now we know that u does not depend on z, it simplifies things. The math now looks like:

$\frac{\partial h}{\partial t} = -(H+h)\frac{\partial u}{\partial x},$

$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} = - g\frac{\partial h}{\partial x}.$

Linearizing, or "throwing out all the beautiful/complicated behaviour" turns these into two coupled equations

$\frac{\partial h}{\partial t} = -H\frac{\partial u}{\partial x},$

$\frac{\partial u}{\partial t} = - g\frac{\partial h}{\partial x},$

that together give the wave equation:

$\frac{\partial^2 u}{\partial t^2} = gH \frac{\partial^2 h}{\partial x^2}.$

The coefficient in that equation is the wave speed squared. So we have, at least from the maths, that the water waves speed increases as the root of the depth. Now let's put it all together and understand why this is.

First of all, how do the waves work? If we raise up a bit of the surface then there is a pressure gradient. This causes fluid to flow away from this crest and as it does so, raise the height of the regions either side of the point we raised. This continues and a wave propagates.

For a given change in surface height, the velocity we pump the water out with is going to be the same. However, the deeper the water, the more of it is being pushed through and so the faster the neighbouring column of water rises.

That is the intuition for the speed, the deeper the water, the easier it is for the height of the surface to be changed by a disturbance and the faster therefore, disturbances propagate.

The set of equations that describe this are called the shallow water equations. They can be derived from the Navier-Stokes equations using the ideas I outlined above. Water waves are a deep topic. Nick Hall has a nice lecture series that introduces the fluid dynamics of ocean waves if you want to learn more.