Lake from a dream: the Fresnel effect

I made a lake in unity! You can scroll down to walk around it in your browser.

The lake is achieved by combining a few different effects. Reflections, small waves on the surface (generated by layering noise at two scales that shifts in time), waves that emanate from the player and the Fresnel effect. This last one is quite interesting.

If you look at the surface of the water at a high angle then it will be more reflective than if you look at it from a shallow angle. You might have never noticed this but it is all around us, and not just on lakes. Try looking at a table from a low and high angle, you will notice it becomes brighter at a high angle. The physics of this effect is surprisingly deep.

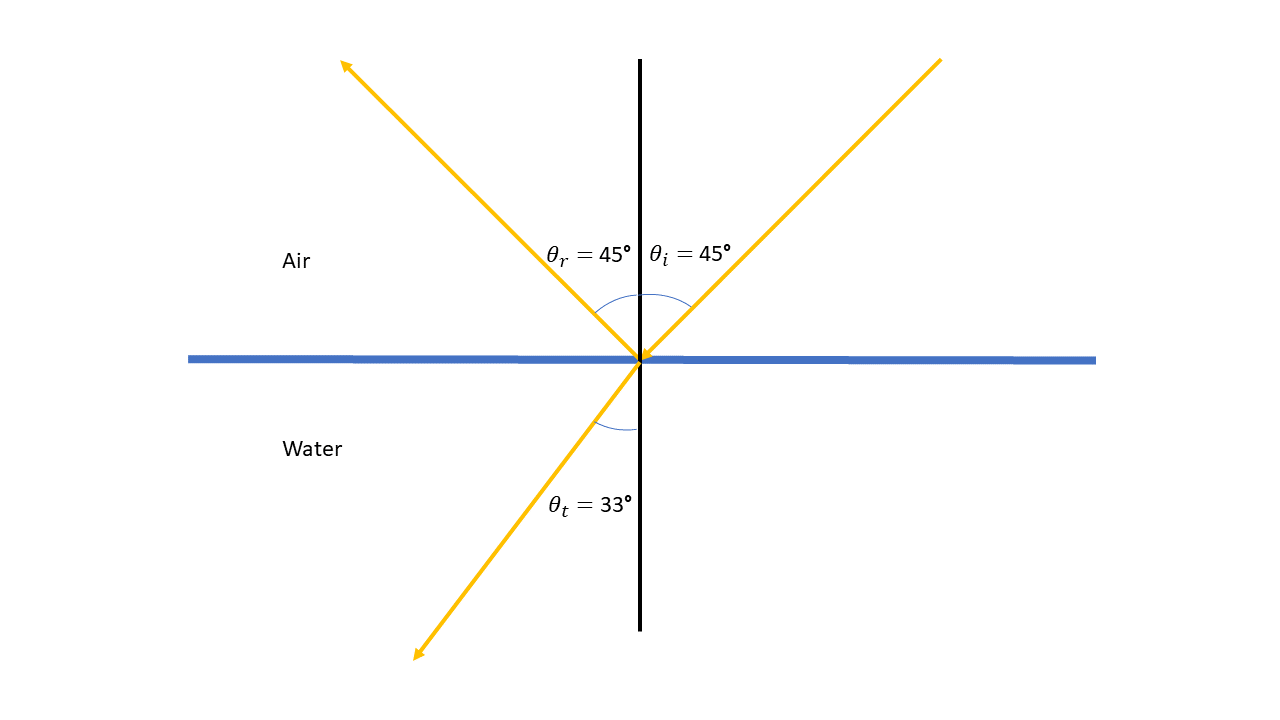
Let's stick with the lake. Light is reflected from the stars onto the mountain. This light then hits the surface of the water. Some of the light is reflected off the surface and some is transmitted into it. The angle the reflected light goes in is easy to figure out, it is always equal to the angle of incidence. The angle of the transmitted (refracted) light requires a little more.

One of the bits of physics everyone learns in high school (and then promptly forgets) comes in handy here. Snell's law gives the angle the refracted light goes relative to the direction perpendicular to the surface. This depends on the indices of refraction, \(n\), of the two materials (in this case air and water). The index of refraction is the ratio of the speed of light in a vacuum (the speed limit of the universe, \(3 \times 10^5 km/s\)) to the speed of light in the medium: \(n = c/v\).

In particular, Snell's law is \(n_1 \sin \theta_1 = n_2 \sin \theta_2\).

If light comes in at an incident angle of 45 degrees, then this tells us that since \(n_{air} \approx 1\) and \(n_{water} \approx 1.3\), the refracted light will shift towards the normal and have an angle of about 33 degrees.

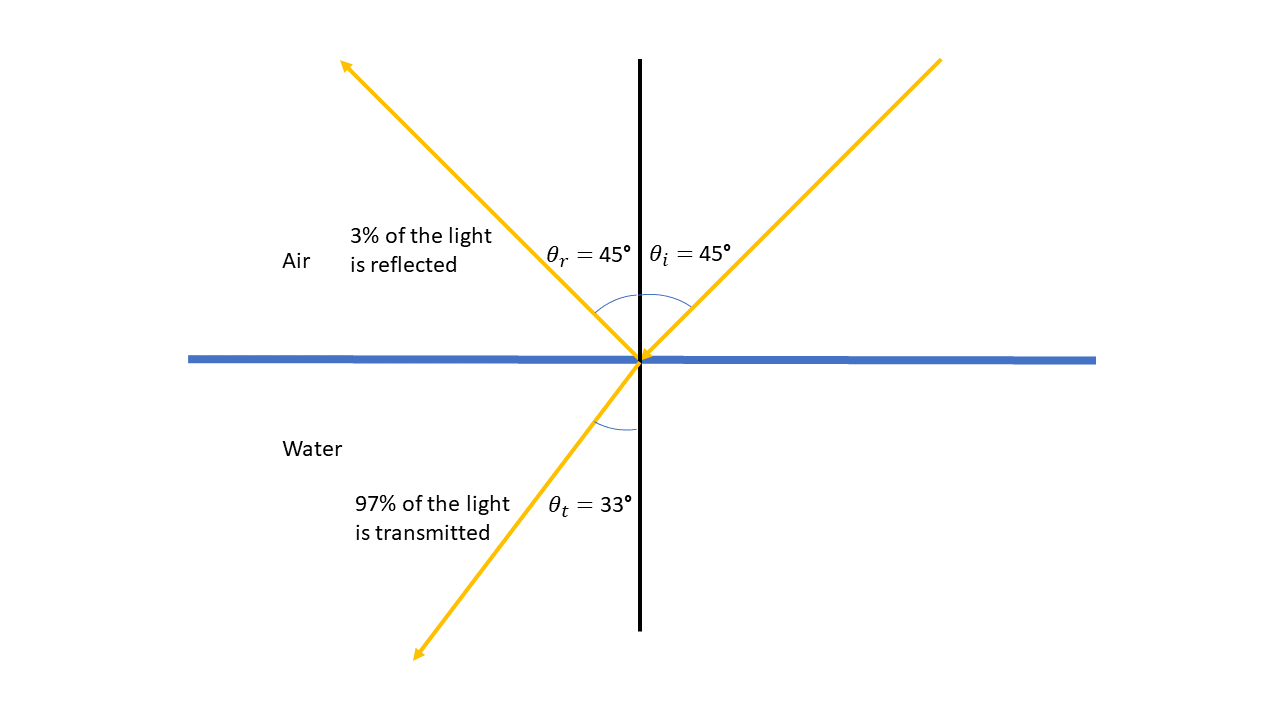
The amount of light refracted and reflected is not equal. It depends on the angle of incidence and the polarisation of the incident light. Assuming the light is not polarised (it contains a uniform mixture of polarisations) and the mediums involved are not magnetic, then the reflectance \(R\) (ie the proportion of the light that gets reflected) is given by the Fresnel equation

\(R = \frac{1}{2} ((\frac{n_1 \cos\theta_i - n_2 \cos\theta_t}{n_1 \cos\theta_i + n_2 \cos\theta_t})^2+(\frac{n_1 \cos\theta_t - n_2 \cos\theta_i}{n_1 \cos\theta_t + n_2 \cos\theta_i})^2) \)

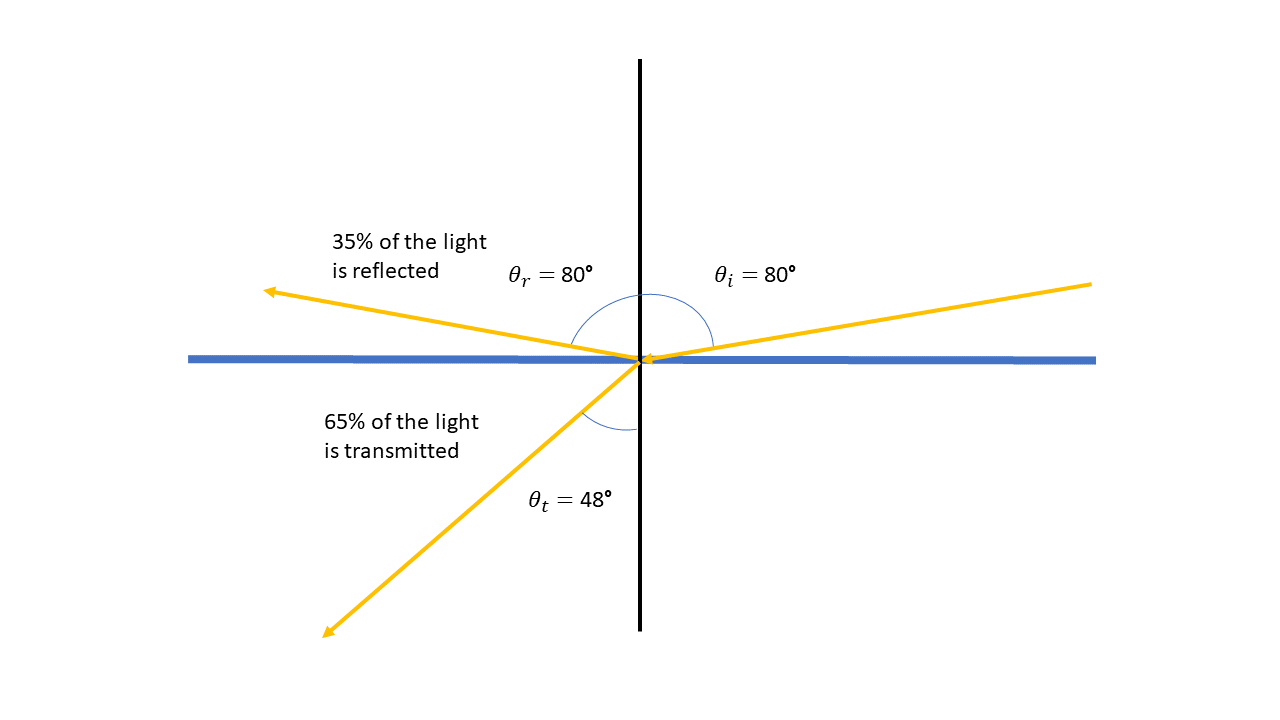
where \(n_1\) is the index of refraction in the material where the incident beam is and \(n_2\) is for the material the light is transmitting into. The next two figures show how the amount of light reflected changes as the angle of incidence steepens:

Why is this happening?

If you did optics in a physics degree you can probably give a much better explanation for the deep reasons for this behaviour than I can. I am not totally satisfied with the answers I managed to find but will leave something here to help scratch that itch of curiosity.

To answer this, we have to start with some more general questions; what is light and why does it slow down when not in a vacuum?

Light is an electromagnetic wave. An oscillating charge will send out ripples in the electric field. The Maxwell equations of electromagnetism tell us that a changing electric field (like the waves the oscillating charge has produced) will in turn cause a magnetic field. They also tell us that a changing magnetic field (as we have just induced with our waves in the electric field) will cause an electric field. In this way, the wave we produce becomes self-sustaining. It will travel forever in a vacuum.

When this wave meets a material, its changing electric field pushes and pulls the charged particles. The electrons respond especially strongly since they are much lighter than their heavier positive neighbours in the nucleus. These oscillating charges produce their own electromagnetic waves which interfere with or enhance the wave that caused them.

So far so good? Well this is actually a simplification. Light behaves both like a wave and a particle. The light is absorbed by electrons as if it were a single particle and then is reemitted.

So, the light is slower because it is being absorbed and then reemitted and there is a delay in this process? Not a bad explanation but also a simplification. In fact, our best understanding of the universe is that the light is simultaneously travelling every possible path through the medium and interacting constructively and destructively with itself.

Backing away from this rather alien reality we can understand the Fresnel effect from the electromagnetic wave perspective of light. When light hits the surface at a low angle (dead on) the electrons oscillate basically in phase with each other. It turns out this means the waves they produce interfere constructively in the forward direction into the medium and destructively away. As the angle steepens the electrons start to become out of phase. The light hits closer electrons before the next electron along. This causes more of the light to constructively interfere in the air and so be reflected.

If that sounds confusing to you then we are in the same boat!

Why not take a break and see if you can spot the Fresnel effect applied to the lake? Don't look too closely at the reflections though!