Fractals, Infinty and AI

Have you ever watched one of those super deep fractal zoom videos? I saw this one in particular back in high school and remember being blown away; how was such beauty being constructed?

I thought that there must be some complicated mathematics that was being used to generate the image but I couldn’t imagine what it could be.

The structure that is being zoomed into above is called the Mandelbrot set. Surprisingly, the formula to generate the image can be written in just a few lines of code and if you know what a complex number is, is very easy to understand.

Before any zooming takes place the image we are looking at is displaying the output of an algorithm applied to a range of complex numbers with real parts from -2 to 1 and imaginary part from -1 to 1, as shown in the figure below.

The algorithm plays a game. It says that if I start with \(0\) then add this number, then square the result and add this number again and square and add repeatedly, does the value blow up?

Symbolically, \(z = z^2 + c\) where \(c\) is our number and the initial value for \(z\) is \(0\).

The points where the value does not tend to infinity are considered inside the Mandelbrot set. If we count how many iterations it takes for points to leave a circle of radius 2 (beyond this value it is impossible to avoid going to infinity) then we can use this to colour the points close to the boundary, this is what the rich colours in the visualisations in this article mean.

As a teenager I was inspired and tried to make my own zoom in java. I think this was one of the first things I tried to program. It was awesome to see the bulbs emerge but I soon realised that I couldn’t zoom in as much as in the video. Honestly, I had already stretched myself to get to that point so I shelved the project.

Recently, I had a discussion with Tjarda Boekholt, a postdoc at Oxford who has made some awesome 3 body problem simulations. We talked about arbitrary precision computing and I realised that this was what was used to catch the fractals is 4k.

Instead of the 64 bits usually assigned to a double in a computer, you can do maths on numbers with arbitrary bits in their representation. This introduces a lot of overheads but allows you to zoom deeper than machine epsilon (the smallest resolvable difference between numbers in double precision).

This video I made shows how far you can get with double precision:

The last frame in both double and arbitrary precision is shown here:

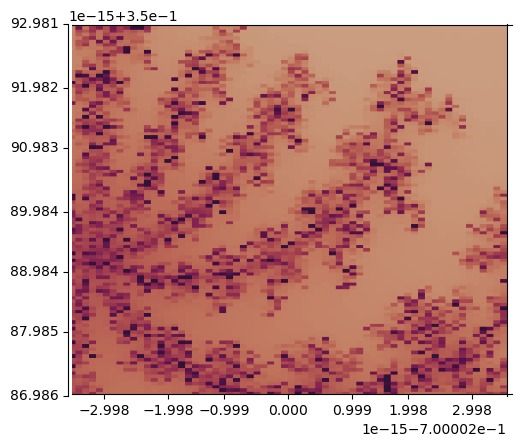
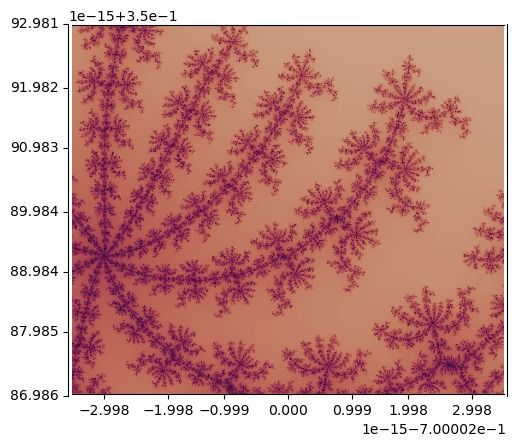
The code can be found on my github here. The creators of the deep zooms must use lower level languages like c and perhaps go to a lot of effort to make it so they can run arbitrary precision on GPUs.

I wanted to make a slightly deeper zoom but I was too lazy to wait for the arbitrary precision code to run. That led me to find out about Misiurewicz points. These are points where the path always repeats eventually.

In the algorithm you always start at \(0\), so after one iteration the value is always \(c\). These points are found by looking for solutions where after n iterations you get back to \(0\) and the cycle must repeat. You can write this algebraically by substituting in \(z^2 + c\) for \(z\) n times and solving the algebraic equation that results.

The cool thing is that around these points you really see the self-similarity of the set. Here is a visualisation for the Misiurewicz point \(i\).

On chatgpt

I used chatgpt when making this project. This was even more interesting than the fractal itself. This was my first time using the AI to write code that I couldn’t write myself.

The skill of programming is becoming obsolete. Now the skill required is the ability to ask the right questions. Putting the long-term implications of this technology aside, this is a wonderful thing. I think it is fair to say that most people have not yet realised it, but it is now possible for noncoders to create amazing things with very little effort.

There is no way I would have succeeded in using cupy (a module in python for using the GPU) to plot the Mandelbrot set without some serious focus and a few more hours of effort than I am willing to admit. Instead, upgrading some code to use cupy took me less than an hour with GPT4.

The world has changed under our feet. Barriers to entry are being torn down everywhere, if you aren’t using AI yet, it’s time to give it a shot.

Not only is AI allowing researchers like me to go further faster than before, but it is giving people who didn’t have the opportunity to explore ideas the ability to do it now. How much faster will science progress?

Until we meet again: