And yet it spins...

Galileo Galilei was the first person to observe the moons of Jupiter. He saw objects in the sky that clearly orbited something other than the Earth.

This observation can lead to a radical thought: Could the Earth be like those moons, could the Earth be orbiting something?

Galileo was persecuted by the Church for advocating the views of Copernicus. For saying that the Earth orbits the Sun.

A day was not the sun rapidly spinning around the Earth, but the Earth rotating on its axis.

For this transgression, he was under house arrest for the last 32 years of his life.

After his trial, having been forced to recant the heliocentric model, he is supposed to have (presumably under his breath) "And yet it moves".

But we can understand why it was confusing for those bishops and beadles. We are on a ball spinning at 1000 mph at the equator, and yet, somehow, it just doesn't feel that way. While the spinning of the Earth doesn't seem to impact us immediately, beyond the day-night cycle, there are in fact several fascinating consequences.

If you can cast your mind back to the last time you were on a merry-go-round at the park you can begin to see why. As the merry-go-round spins faster you are more and more liable to be flung off. This is due to the centrifugal force and is why you have to hang on to the ride.

The centrifugal force acts perpendicular to the axis of rotation. That means that at the equator it points directly upwards but everywhere else, some component of the force is horizontal to the ground.

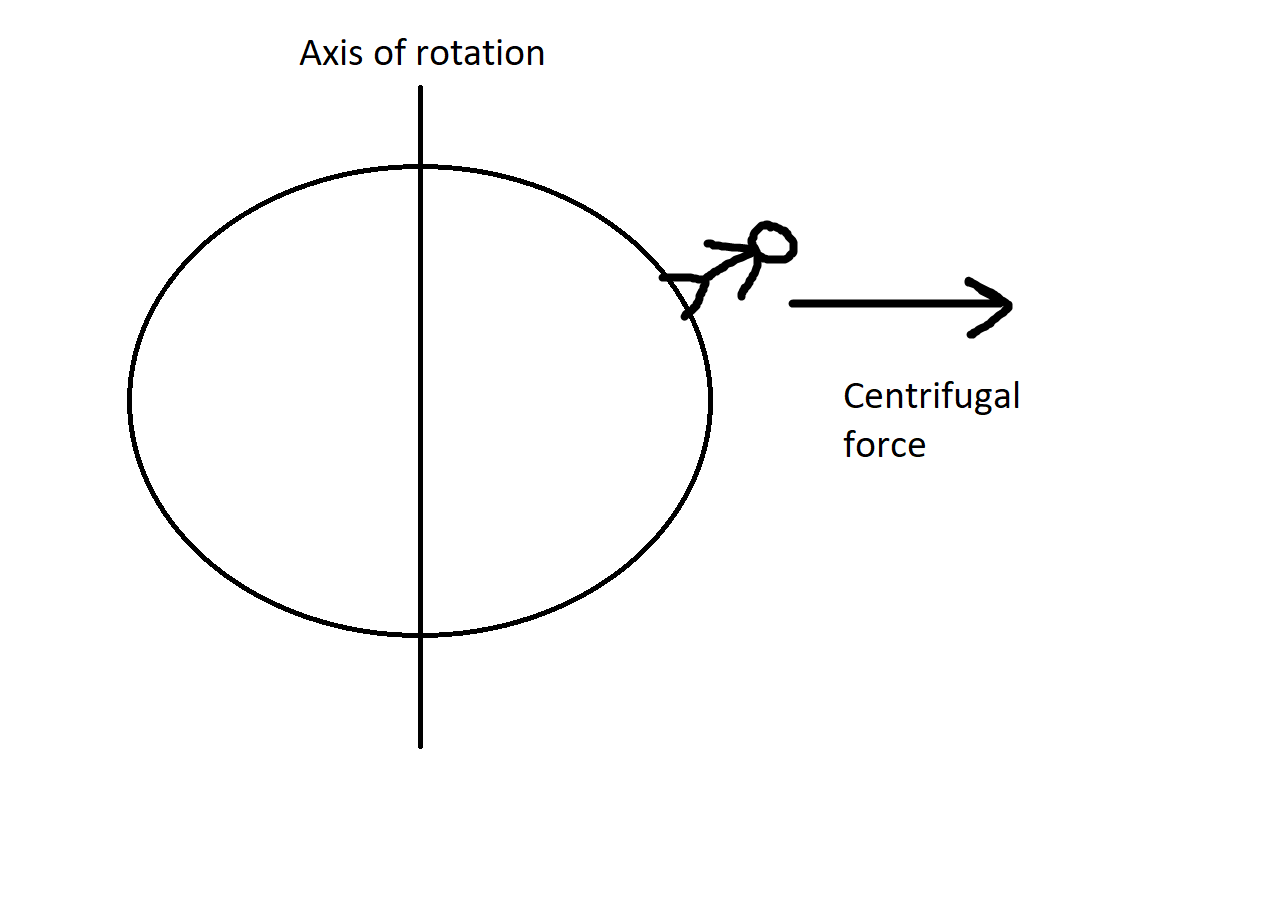
How big is this force?

Thankfully, we are not all being dragged towards the equator and flung into space. The Earth would need to spin about 20 times faster for that. Here is a graph showing the strength of the centrifugal force for different latitudes:

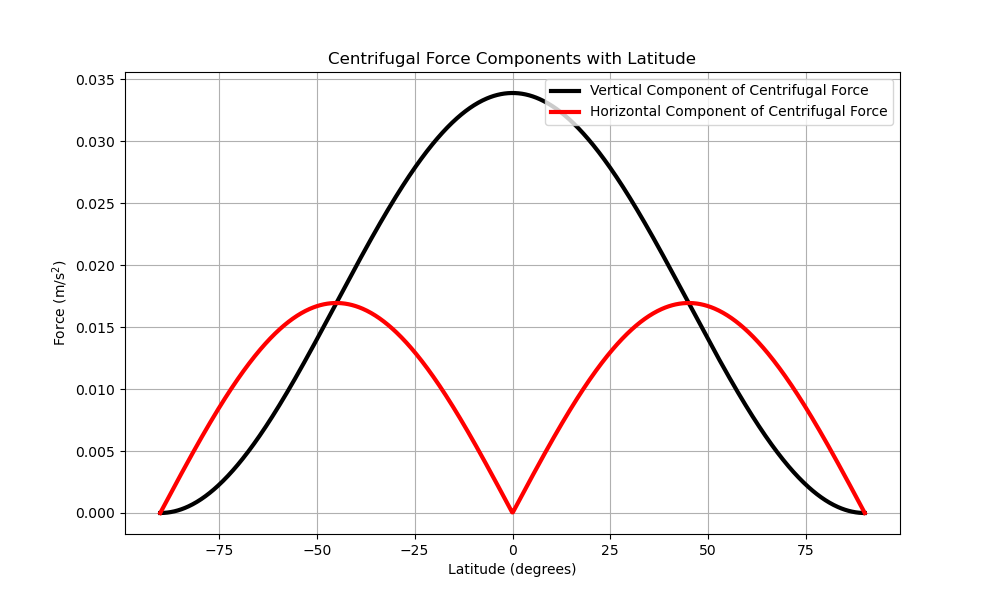
This means the typical person will feel about 250 grams lighter at the equator than at the pole! It also means that we are feeling about a Newton of force (the same amount of force required to pick up an apple) pushing us towards the equator!

If someone were to push you with that amount of force you would certainly feel it, so why can we not all innately know which way goes to the equator?

The answer is that the Earth has been at this a lot longer than us. The ground has adjusted in such a way that up is not directly up from the center of the planet, but rather up relative to the effective gravity (gravity and the centrifugal force combined), so we feel no directional force.

This is why pedants like to say the Earth is not a sphere, it's an oblate spheroid. Those extra inches around the waist mean gravity is even weaker at the equator than we stated earlier, giving you another 250 lost grams on the scale.

There's another interesting thing that arises from the spinning. To see what it is, let's go back to the carousel at the park.

Suppose you were to throw a ball in a straight line while you were riding the carousel. To anyone watching from the park, the ball would go straight, but since you move while it is in motion, its trajectory won't look straight to you. If you were spinning fast enough, you could even hit yourself in the face with the ball you threw!

This is the Coriolis force. It is a pseudo-force. Nothing is producing a force on the ball to make it move in a circle and hit you in the face, it simply appears that way from your perspective. In reality, you just spun into the innocent ball as it was minding its own business.

The Coriolis force due to the Earth's rotation is pretty hard to spot at the human scale; the thing about toilets flushing in different directions in the two hemispheres is false. But at the largest scales, it is of foremost importance.

The Coriolis force is given by \(F = -2m\mathbf{\Omega} \times \mathbf{v}\) where \( \mathbf{v}\) is your velocity and \(\Omega\) is the rotation vector. If you don't come from a math background, the essence of it is this: the force pushes you at a right angle to the direction you are moving (the right in the northern hemisphere), it will only act on you if you are moving, and the faster you go, the stronger it is.

Naval guns and long-range artillery all have to account for this effect. In theory, long-range sniper shots also need to account for Coriolis. I believe this doesn't happen in practice due to the effect being lost in the noise of the wind. I am no expert sniper though, get in touch!

Vast amounts of air and water are constantly in motion in the atmosphere and ocean. These grand motions are hugely affected by the Coriolis force.

If you are old-school enough to look at weather maps, you would see pressure contours. The wind does not go from low to high pressure, which is what you would expect in a room for instance. Instead, the Coriolis force deflects it so that the wind turns so much it goes along pressure contours!

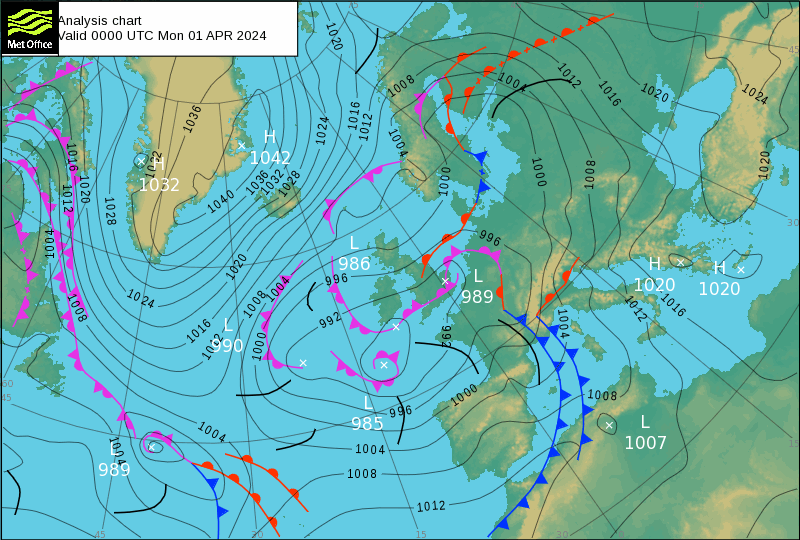
So there you go, I hope that didn't make your head spin!