Beauty that computers can’t capture (for now)

Can a computer write a symphony, can a computer turn a canvas into a beautiful masterpiece?
Well... yes.
We have reached an era of AI art and music generation. But what can our silicon friends not do? I give 3 examples that came to mind.
The first is mathematical. We cannot represent all the numbers between 0 and 1 in a computer simply because computers are limited to finite representations of numbers. This is a shame because funky things happen when we let irrationals come out to play. An example is the famous Banach-Tarski paradox. This paradox says that we can construct two identical balls from a single ball by cutting it in a particular (100% not physically possible) way.
The second is a matter of time. We have AI art and music generation, but what about AI feature movie generation? I talk a bit about how incredible image generation is, the basic idea of how they work and where they might be heading.
The last is experience itself. If our computer were to have a conscious thought, would we know? If we ran an algorithm and the computer felt something would it ever be possible for us to know what that something was? I speculate a bit about this possibility.
The logistic map
The logistic map is a wonderful toy model. It represents the growth and decay of a population as you vary a kind of “boom or bust” parameter. You can think of it as how excitedly members of the population reproduce when times are good and how quickly they die when times are bad all rolled into one. I will just call it the sensitivity parameter. A high number means both things happen vigorously.
Strangely, we are going to allow the population to be any number between 0 and 1. Maybe you could think about it as the percentage of the population that is alive out of some maximum possible population, but that percentage can be as close to 0 as you like.
Another key thing to realise about the model is that it is discrete. The population is not varying smoothly, it is updated in one go. It would be like if everyone read the newspapers for a year and then on the 1stof January decided whether to have a child or die.
Why is such an arbitrary model interesting?
It demonstrates behaviour that is in some sense universal and represents a cornerstone of a part of mathematics called Chaos theory. Yes, that’s what Jeff Goldblum’s mathematician in Jurassic Park was researching.
The figure below is taken from Wikipedia. On the horizontal axis is the sensitivity parameter, on the vertical axis is the population. Plotted is what values the population takes after some time has passed.
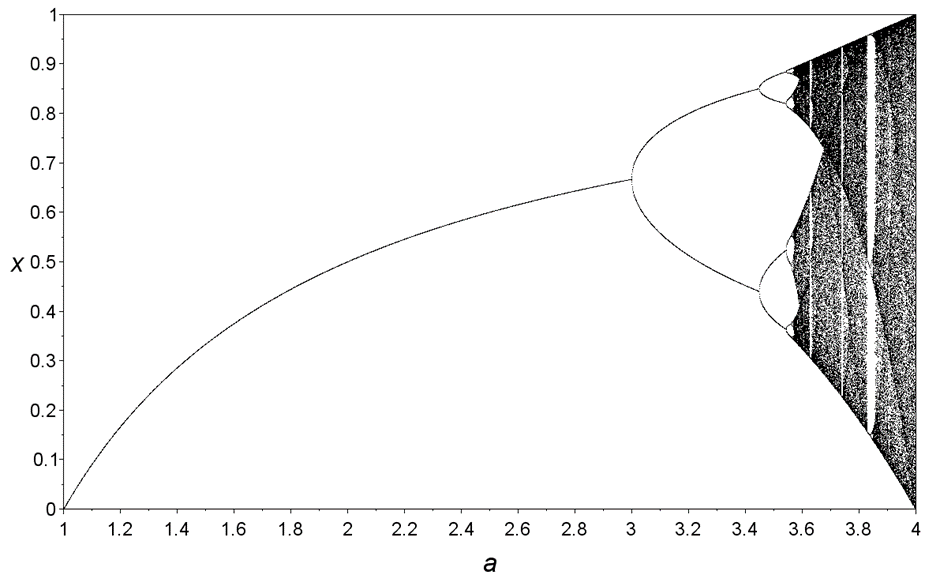
Let’s take a moment to get our heads around this. We start with a population near 0. If we are not so sensitive then the population simply increases until we reach an equilibrium. The number of kids being born is balanced by the amount of people dying.
This is what is going on until the sensitivity reaches 3. For systems more sensitive than this, (3 < a < 3.44…) the population will eventually oscillate each year between two different values. A bit more, and it will oscillate between 4 different values, a little more, 8, a little more 16 and so on.
But do you see those white stripes among the black dots? Those are not some artefact of scanning an image, there are regions of stability, at some point, instead of oscillating between millions of values it oscillates between 3, or 5 or some other number.
This is all beautiful (to some people, me included) but there is something extra that cannot be represented. That equilibrium population from before we turned up the sensitivity is still possible. The system can reach it, but not on a computer. In fact, there are an infinite number of starting points where if we were to initialise the population there, it would end up at that equilibrium. There is also an infinite number of points where it will end up at the oscillation between two values. As the sensitivity is increased, these options are drowned out by the more dominant outcome. The mental image of an arbitrarily small interval within which you could end up on any cycle is something that is relegated to our imaginations.
There are many systems that experience a similar period doubling cascade. An example is water dripping out of a tap. These all have these unstable fixed points that computers are almost never able to resolvable.
In more mathematical language, our computer cannot resolve the unstable manifold.
Within this class, which in some sense boils down to thinking about infinities of subdivision, there are also mathematical ideas like the Cantor set and the related Banach-Tarski paradox.
The perfect movie
The screen you are viewing this on has some number of pixels. If it is a laptop it has something like 2000 pixels horizontally and 1000 vertically. That is 2 million total pixels, each with 3 colour channels, red, green and blue. Those channels can be mixed in different ways and in the standard setup, each pixel can have about 17 million possible colours. The number of possible ways you could combine these is mind numbingly enormous.
It has to be.
Every frame of every movie, every page of every book, every family photo you ever took and everything anyone ever saw and didn’t see is somewhere in that sea of possibilities.
So why don’t we reach out and grab some of these from the ether?
They are there, after all. Waiting to be discovered. Our first attempt can be to put random values for the colour into every pixel. The result is predictable, somewhat surprisingly given the limitless sea of possibilities. We see nothing, noise and chaos.
But what if we had some kind of mathematical machine that could guide us to interesting places in the noise? That is what image generation AIs are. It is simply breath-taking that they work at all.

A function in maths takes in an input and gives an output. Squaring x is a function. Give me a number x and the function returns the square of that number. You give me 5, I give you 25. There is a function that would give me a wave, the sine function. There is also a function that if you gave me some random noise, would tell me what numbers to add to that noise to move closer to an image of a cat.
A neural network is a function chameleon. It uses linear algebra and a nonlinear activation function (otherwise you could only mimic a linear function) to mimic any possible function. The key is you can force the clay to form the function you desire by using a technique called steepest descent. If you have some way of measuring the performance of your model, then you can figure out what nudge to all the little dials in the neural network you need to make to make it act more like the function you are chasing.
Our mathematical machine for finding images in state space is then simply a function that can match images to written captions. The OpenAI program that does this is called CLIP. Image generators usually use methods such as stable diffusion, which means adding a step where you can generate variations on an image but that isn’t really important to the general idea of how they work.
Image generators are a hot topic and there seem to be breakthroughs every few months. For now though, soaring through feature length movie state space on the search for a Shawshank Redemption remains out of reach. Entertainers across the globe can rest easy, for now.
What it feels like to do computation
Does a computer feel anything? Probably not. But we do, and we have memories and the feeling of “being alive”. What is the difference between us and a computer?
In a computer, information is held in binary 1s and 0s. To encode the number 12 for example, there will be, somewhere in the computer 1100. This uses powers of two to create 12 (here one 8 plus one 4 plus no 2 plus no 1 is 8+4=12). You could hold 1100 in the computer as 4 LED lights, the first 2 are on and second 2 are off.
If the lights are controlled by little switches (called transistors) then if I went at my computer with a scalpel and cut these switches out, 12 would vanish from its memory.
Incredibly, it is not possible to do the same to a person.
In the 1940s Karl Lashley was putting mice through mazes. By training mice to know how to navigate a maze he had a way to prove the mice remembered something. He would then cut parts out of their brains. Amazingly, he concluded that the memory was not stored in one part of the brain, but was rather distributed across the whole cortex. As you cut parts out of a mice’s brain they would get worse at learning new things, but still retain the intact memory of how to navigate the maze.
This implies that memory and perhaps our conscious experience with it, are emergent from the interactions of those millions of electrical switches known as neurons, rather than having a specific home in the brain.
But what if we could recreate this emergent phenomenon using transistors instead of neurons? Supposing it is the connections of neurons and not something about their physical nature that leads to consciousness and memory, it would then be possible, in principle, to simulate the brain using a computer. Would our simulation of a human mind be conscious?
There is currently no way for us to tell what our computer is feeling. Even the notion sounds ridiculous. However, with projects like Neuralink and its successors, the concept of receiving feelings as output from a computer may not seem so strange one day.
I can think of a lot of ways for that to go wrong.




Comments ()